
|
|
 Grafy a grafové algoritmy III.
Grafy a grafové algoritmy III.
Tento článek volně navazuje na článek Grafy a grafové algoritmy II, ve kterém byl řešen problém nalezení minimální kostry grafu. Tento článek se také zabývá minimální kostrou, tentokrát je ale minimální kostra hledána na orientovaném grafu, k čemuž slouží Edmondsův algoritmus.
22.4.2011 00:00 | Petr Sklenička | read 16584×
DISCUSSION
Úvod do orientovaných grafů
Z minulých článků už je nám znám pojem graf, vážený (ohodnocený graf), kostra grafu apod. Doposud jsme však neměli možnost setkat se s tzv. orientovanými grafy. Pojďme si tedy tento pojem neformálně přiblížit.
Doposud jsme se setkali s takovými grafy, že pokud mezi libovolnou dvojicí vrcholů a a b vedla hrana,
znamenalo to, že bylo možné "jít" v grafu jak z vrcholu a do b, tak i opačně, tedy z b do a.
U orientovaných grafů toto již není možné. U každé hrany je totiž uveden i její směr. Ohodnotíme-li navíc každou hranu
(čili určíme její váhu) dostaneme ohodnocený orientovaný graf. Ještě jednou tedy podotýkám následující:
Hrana (u, v) v orientovaném grafu G začíná ve vrcholu u a končí (též směřuje) ve vrcholu v.
Opačná hrana, tedy (v, u) je jiná než hrana (u, v).
Minimální kostra orientovaného grafu
Myslím, že nyní je pojem orientovaného grafu jasný, proto přejdeme dále. Náplní tohoto článku je algoritmus, který dokáže najít minimální kostru takového grafu. Jistě si vzpomenete, že v minulém článku jsme také hledali kostru, jednalo se však o neorientované grafy. Ukázali jsme si Kruskalův a Jarníkův algoritmus - ani jeden z nich na orientovaném grafu nefunguje. Obecně vzato, nalezení minimální kostry orientovaného grafu je úkol o poznání složitější a náročnější, než hledání minimální kostry neorientovaného grafu, což je pak samozřejmě vidět i na celé implementaci. Algoritmus, který řeší náš problém, se nazývá Edmondsův algoritmus. Než však přejdeme k samotnému algoritmu, podívejme se ještě na to, jak vypadá kostra orientovaného váženého grafu.
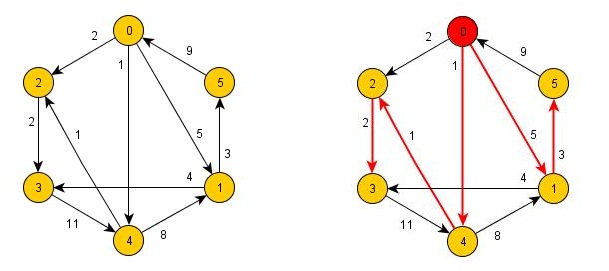
Všimněte si, že jeden z uzlů je označen červenou barvou. Tomuto uzlu se říká kořen. Je nutné mít na paměti, že kostra grafu je strom (pozn.: Pokud jste nečetli článek Grafy a grafové algoritmy II, doporučuji si jej přečíst, neboť tam je vysvětleno, co je to strom, kostra, minimální kostra apod). Otázkou tedy je, co je to kořen. Neformálně řečeno, je to uzel, ze kterého celý výsledný strom "vyrůstá". Lze jej také pokládat za začátek stromu. Kořen nemá žádného rodiče, má pouze potomky, kteří zase mají své potomky a tak dále. Způsob, jakým v nějakém stromu najít vhodný uzel, který by reprezentoval kořen, zde rozepisovat nebudu, pouze naznačím, že to souvisí s nalezením tzv. centra stromu. Nyní se vraťme k algoritmu.
Nejprve si ujasněme, jakým způsobem uložíme vážený orientovaný graf do počítače. Není to nikterak složité, postačí nám k tomu
obyčejné, dvourozměrné pole. Nazvěme jej G[i][j], kde i odpovídá počtu hran a j bude rovno
třem.
| Počáteční vrchol | Koncový vrchol | Váha |
| 0 | 2 | 2 |
| 0 | 1 | 5 |
| 0 | 4 | 1 |
| 1 | 3 | 4 |
| 1 | 5 | 3 |
| 2 | 3 | 2 |
| 3 | 4 | 11 |
| 4 | 1 | 8 |
| 4 | 2 | 1 |
| 5 | 0 | 9 |
Uvedená tabulka zachycuje, jakým způsobem budou data uspořádána v dvourozměrném poli. V řádku je nejprve uveden vrchol, ve kterém hrana začíná, následuje koncový vrchol a poté váha hrany. Můžete si všimnout, že tabulka odpovídá grafu, který je na obrázku výše. Celý kód, který je mimořádně v jazyce Java, si můžete stáhnout zde. Podotýkám, že v kódu je použito několik datových struktur - u každé struktury je komentář, k čemu slouží. Celý algoritmus je poměrně komplikovaný, proto pokud mu chcete opravdu porozumět, nestačí si jen přečíst následující stručný popis, ale také je nutné projít si kód a snažit se ho pochopit, což nemusí být až tak snadné. Nakonec ale musím přiznat, že mě v tuto chvíli nenapadá přilíš reálných situací, kdy by bylo potřeba tento algoritmus použít, narozdíl třeba od algoritmů, které hledají kostru neorientovaného grafu, nebo slouží k nalezení nejkratší cesty v grafu.
Celý algoritmus lze rozdělit na dvě části. V první části se všechny uzly nachází v roots (obsahuje komponenty,
do kterých zatím nevede hrana). Z roots se náhodně vybere nějaký uzel (x) a pro tento uzel se také vybere nejkratší hrana,
která do něj vede (vrchol, ze kterého hrana vychází, označíme y). Jestliže taková hrana neexistuje, potom je jasné,
že uzel bude kořen aktuálního stromu. Pokud taková hrana existuje, algoritmus tuto hranu buď zpracuje, nebo se vrátí na
začátek a vybere jiný uzel. Rozhodujícím faktorem, který z těchto dvou případů nastane, je otázka, zda jsou uzly x a y ve stejné
silné komponentě. Pokud ano, algoritmus se vrací a vybírá jiný uzel. Jestliže jsou ale uzly x a y v různých slabých komponentách,
algoritmus tyto komponenty spojí a vrátí se na začátek. Pokud jsou uzly x a y ve stejné, slabé komponentě, pak vznikne nová
silná komponenta. V tuto chvíli je nutné vstupním hranám snížit jejich prioritu o rozdíl aktuální váhy a maximální váhy, přičemž
maximální váha je váha maximální hrany. Po přehodnocení hran se sloučí haldy hran uzlů v nové komponentě a algoritmus se vrátí
opět na začátek.
Celá první část algoritmu defakto udělala to, že vyfiltrovala "zbytečné" hrany, čili ty, které v kostře zcela jistě nebudou.
Máme tedy pouze seznam hran, které v kostře být mohou. Dále máme množinu kořenových uzlů minimálního lesa (les je jednoduchý
graf, který neobsahuje kružnice). Dále zavedeme prázdnou množinu hran, např. A. Poté stačí opakovat následující kroky (1, 2, 3) do doby, dokud množina
kořenových uzlů minimálního lesa a množina fRoots (kořenové uzly lesa) nebudou prázdné.
- Pokud je množina kořenových uzlů minimálního lesa neprázdná, odstraníme jeden z jejích prvků. Pokud je prázdná, pak odstraníme
vrchol z množiny
fRootsa přidáme jej do množiny A. - Dále algoritmus identifikuje cestu mezi listem (vrchol, který nemá žádné potomky) lesa (tj. vrchol z množiny
fRoots) a kořenem lesa (opět vfRoots). - Nakonec odstraníme z
fRootsty uzly (a samozřejmě z nich vycházející hrany), které byly identifikovány v předchozím kroku. (2)
Několik slov závěrem
Jistě sami vidíte, že Edmondsův algoritmus je například v porovnání s Kruskalovým algoritmem mnohonásobně složitější. To je samozřejmě dáno tím, že Kruskalův algoritmus nebere v úvahu, že by hrany mohly být orientované. Oproti tomu ale nalezení kostry neorientovaného grafu je přece jen úkol, který se vyskytuje častěji, než úkol nalezení kostry orientovaného grafu. Proto si osobně myslím, že není nikterak nutné umět napsat Edmondsův algoritmus "z hlavy na jeden zátah". Na druhou stranu určitě není na škodu vědět, že takový algoritmus existuje, vědět k čemu slouží a alespoň trochu tušit, jak zhruba funguje.
|
|
||
|
DISCUSSION
For this item is no comments. |
||
|
Add comment is possible for logged registered users.
|
||
| 1. |
Pacman linux Download: 5778x |
| 2. |
FreeBSD Download: 10005x |
| 3. |
PCLinuxOS-2010 Download: 9500x |
| 4. |
alcolix Download: 12050x |
| 5. |
Onebase Linux Download: 10742x |
| 6. |
Novell Linux Desktop Download: 0x |
| 7. |
KateOS Download: 7188x |
| 1. |
xinetd Download: 3326x |
| 2. |
RDGS Download: 937x |
| 3. |
spkg Download: 6340x |
| 4. |
LinPacker Download: 11584x |
| 5. |
VFU File Manager Download: 3945x |
| 6. |
LeftHand Mała Księgowość Download: 8269x |
| 7. |
MISU pyFotoResize Download: 3653x |
| 8. |
Lefthand CRM Download: 4475x |
| 9. |
MetadataExtractor Download: 0x |
| 10. |
RCP100 Download: 4008x |
| 11. |
Predaj softveru Download: 0x |
| 12. |
MSH Free Autoresponder Download: 0x |
 linuxsoft.cz
| Design: www.megadesign.cz
linuxsoft.cz
| Design: www.megadesign.cz