ARCHIV

C++ Binární vyhledávací stromy

V tomto článku se podíváme na binární stromy. Řekneme si tedy, co vlastně binární strom je, proč se používá, probereme si některé operace, které se nad binárními stromy provádějí a nebude chybět ani ukázka některých metod v jazyce C++.

9.11.2010 00:00 | Petr Sklenička | Články autora | přečteno 27729×

Úvod do binárních stromů

Binární strom je datová struktura, která se skládá z několika uzlů, přičemž každý z nich má maximálně dva potomky (proto binární strom). Takto by se dal jednoduše definovat binární strom, pro lepší představu se však podívejte na následující obrázek.

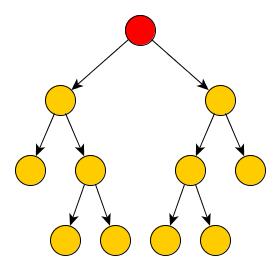
Všechny "kroužky", které na obrázku vidíte, se nazývají uzly stromu. Speciální případem uzlu je červený kroužek, kterému se říká kořen stromu. Kořen stromu jako jediný nemá žádného rodiče, zjednodušeně řečeno, není nad ním žádný uzel. Dále si na obrázku všimněte, že ne každý uzel má právě dva potomky. To však není v rozporu s naší definicí, proto se opravdu jedná o binární strom. Dále si zavedeme pojem hloubka uzlu - jde o délku cesty od kořene k danému uzlu. Největší hloubka libolného uzlu se pak označuje jako výška stromu.

Binární vyhledávací stromy

Nyní, když víme, co je to binární strom a máme zavedeny nejdůležitější pojmy, můžeme se podívat na binární vyhledávací stromy. Jedná se o speciální případ binárních stromů, kdy každý uzel obsahuje nějaký klíč, na jehož základě je definováno nějaké uspořádání. Celý problém lze říci i jednodušším způsobem - v každém uzlu stromu je nějaká hodnota a platí, že v levém podstromu jsou hodnoty menší, naopak v pravém podstromu jsou hodnoty větší. Aby to bylo úplně jasné, nakreslíme si strom, který vznikne postupným přidáváním těchto prvků: 9, 12, 10, 24, 3, 0, 30.

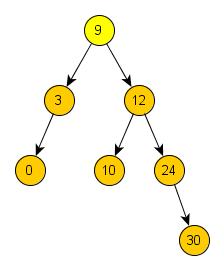
Kořen stromu je 9. Dále jsme přidali číslo 12, které je větší než 9, proto je číslo 12 na pravé straně pod číslem 9. Následovalo číslo 24, které je větší než 9, je také větší než 12 a proto je číslo 24 pravým potomkem čísla 12. Číslo 3 je menší než 9, je tedy levým potomkem čísla 9. Tímto způsobem jsme do stromu uložili i další zbylá čísla. Je snad tedy jasné, že při přidávání prvků do binárního vyhledávacího stromu začínáme od kořene a postupujeme podle toho, zda je číslo menší nebo větší.
Použití binárních vyhledávacích stromů je velké, jako úplně nejjednodušší příklad lze uvést toto: Máte v textovém souboru uloženo 10 000 000 čísel. Mezi těmito čísly potřebuje nějaké vyhledat. Někoho by napadlo, že si čísla uloží do pole a poté bude pole prohledávat. Pokud by prohledával metodou "pokus omyl", čili by procházel prvky hezky postupně za sebou, mohl by mít tu smůlu, že jeho číslo by bylo úplně až na konci pole, tudíž by potřeboval 10 000 000 porovnání. To je v dnešní době počítačů poměrné dlouhá doba. Metoda půlením intervalu by byla jistě efektivnější, jenže aby fungovala, muselo by se pole nejprve setřídit, což také nějakou dobu potrvá. V případě, že bychom ale čísla uložili do stromu, maximální počet porovnávání by byl roven výšce stromu, která by v 99 procentech případů nebyla 10 000 000. Binární vyhledávací stromy tedy slouží k jakési organizaci dat s následných rychlejším vyhledáváním.

Implementace binárního vyhledávacího stromu

Jestliže již tedy víme, jak vypadá binární vyhledávací strom a jaké je pravidlo pro přidávání prvků, nezbývá nic jiného, než vymyslet, jak binární vyhledávací strom uložit do paměti počítače. Víme, že strom je tvořen několika uzly, proto si můžeme napsat třídu, která nám takový uzel bude reprezentovat. Každý uzel ve stromu obsahuje nějaký klíč, data (záleží na povaze aplikace) a také si pamatuje svého levého a pravého potomka. Levý a pravý potomek opět není nic jiného než zase uzel.

Pozn.: Předpokládá se základní znalost syntaxe C++, znalost OOP a rekurze.

class Node { private: int key; Node* left; Node* right; public: Node(int x); bool Search(int x); void Insert(int x); void Remove(int x); int GetMax(); int GetMin(); };

Takto jednoduše by mohla vypadat třída uzel. Metod, které obsahuje, si prozatím nevšímejte, hned se k nim dostaneme. Třída uzel obsahuje proměnnou key, do které bychom v našem případě uložili nějaké číslo. Dále obsahuje dva pointery (nebo chcete-li ukazatele) - jeden slouží jako ukazatel na levého potomka, druhý na pravého potomka. Celý strom se potom skládá z několika instancí třídy Node, přičemž pointery left a right ukazují na dané uzly, neboli na objekty třídy Node.

Konstruktor třídy

Náš konstruktor přebírá jeden parametr typu int, který nám reprezentuje číslo, které uzel obsahuje. Číslo x se tedy v konstruktoru přiřadí do členské proměnné key. Dále se v konstruktoru musí nastavit pointery left a right. Vytvoříme-li ale nový uzel, nemá ještě žádné potomky - proto pointery nastavíme na NULL. Celý tělo konstruktoru je velmi snadné, takže jej určitě dokážete napsat sami.

Přidávání prvků do stromu

To, podle jakého pravidla se do stromu přidávají prvky, jsme si už řekli, ve stručnosti si to ale ještě připomeneme. Začíná se od kořene, kde zjišťujeme, zda je číslo, které chceme přidat, větší nebo menší, než číslo, které obsahuje kořen. Podle toho se rozhodneme pro pravou či levou stranu a celý tento postup se opakuje na dalších uzlech do doby, než najdeme to správné místo pro přidávaný prvek. To poznáme tak, že narazíme na uzel, který nebude mít potomka na té straně, kam budeme chtít prvek přidat - pointer na danou stranu bude mít hodnotu NULL. V té chvíli přidáme prvek do stromu a prvek je úspěšně přidán. Nyní se podívejte jak to lze realizovat v kódu.

void Node::Insert(int x) { if (x > this->key) { if (this->right == NULL) this->right = new Node(x); else this->right->Insert(x); } else { if (this->left == NULL) this->left = new Node(x); else this->left->Insert(x); } }

Metoda je napsána tak, že pokud bychom náhodou chtěli přidat prvek, který již ve stromu je, bude tento prvek zařazen na levou stranu. Klidně by se dalo napsat, aby se uložil na pravou stranu, nebo aby se neuložil vůbec. Vidíte, že v metodě je použita rekurze. Pokud Vám není jasné proč, přečtěte si znovu předchozí odstavec, kde se píše o tom, že se nějaký postup opakuje na dalších uzlech. V tom je skryto použití rekurze. Nicméně celou metodu lze přepsat za pomocí cyklu.

Vyhledávání prvků

Vyhledat prvek v binárním stromu je velmi snadné. Algoritmus je příjemně jednoduchý, věřím tomu, že někteří z Vás už ví, jak na to. Začneme tím, že srovnáme hledané číslo s číslem kořenu. Mohou nastat tři možnosti:

Mazání uzlů

Už jsme si řekli, jak prvky do stromu přidat a jak je následně vyhledat, zatím však ještě nevíme, jakým způsobem prvky ze stromu smazat. Nejprve je nutné daný prvek ve stromu najít. Potom, co jej najdeme, můžeme přejít k samotnému smazání. Jak na to? To, že se k tomu používá klíčové slovo delete je snad jasné, nicméně otázkou zůstavá, jak prvek smazat, aby přitom zůstala zachována stromová struktura. Případ mazání prvku si můžeme rozdělit do tří skupin.
1. Mažeme uzel, který nemá žádného potomka
V tomto případě se jedná o velmi jednoduchou záležitost. Uzel, který nemá žádného potomka, můžeme bez problému odstranit a nehrozí, že bychom přišli o nějaké další uzly. Žádné další uzly totiž pod tímto uzlem nejsou.
2. Mažeme uzel, který má právě jednoho potomka
V tomto složitějším případě již nemůžeme uzel jen tak odstranit. Pokud bychom to udělali, přišli bychom i o jeho potomka. Potomek by sice čistě teoreticky zůstal v paměti počítače, nebylo by však možné se k němu dostat, protože bychom na něj ztratili ukazatel. Proto tedy celou situaci musíme vyřešit tak, že vezmeme potomka rušeného uzlu (nezáleží na tom, zda je levý, nebo pravý) a napojíme na něj ukazatel z rodiče rušeného uzlu. Jde si to představit tak, že rušený uzel "obejdeme".
3. Mažeme uzel, který má dva potomky
Jde o nejsložitější případ mazání uzlu ze stromu. Pro lepší vysvětlení si uzel, který chceme smazat, označme například "a". Uzel "a" má dva potomky a nezapomeňte, že i tito potomci mohou mít další potomky. Čím tedy nahradit uzel "a"? Jednoduše řečeno, uzel "a" nahradíme nejpravějším uzlem z levého podstromu uzlu "a", nebo nejlevějším uzlem z pravého podstromu. Kdybych to měl převést do jednoduché formy, řekl bych, že z uzlu "a" se vydáme na libovolnou stranu a hned poté půjdeme na stranu druhou, dokud nedojdeme na konec. Pro názornější pochopení se podívejte na obrázek.

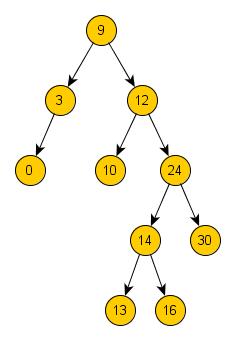
Zkusme si smazat uzel s číslem 12. Budeme jej nahrazovat nejlevějším uzlem jeho pravého podstromu, což znamená uzlem s číslem 13. Z uzlu číslo 12 jsme udělali jeden krok doprava a poté jsme postupovali pořád doleva, až jsme došli k uzlu s číslem 13. Po odebrání uzlu s číslem 12 bude strom vypadat takto:

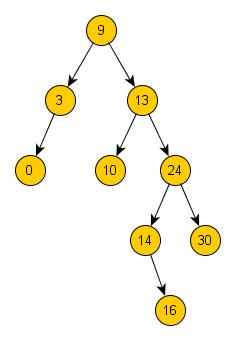
Můžete vidět, že způsob uspořádání uzlů ve stromu zůstal zachován. Mazání uzlů ze stromu tedy není vůbec nic těžkého, stačí pouze vědět, jak postupovat v daném případě.

Nalezení největšího prvku

Někdy se může stát, že potřebujeme zjistit, jaký největší prvek se ve stromu nachází. Pokud se podíváte na organizaci prvků v binárním vyhledávacím stromu, zjistíte, že najít největší prvek je velmi snadné - nachází se totiž úplně vpravo. Stačí tedy od kořene postupovat směrem doprava, dokud nenarazíme na uzel, který již pravého potomka mít nebude. V tu chvíli jsme našli největší prvek.

int Node::GetMax() { if (this->right == NULL) return this->key; else this->right->GetMax(); }

Myslím si, že způsob, jak najít nejmenší prvek je zcela jasný, proto to zde ani nebudu rozebírat.

Průchody stromem

Poslední častou operací, která se nad binárními stromy provádí, je průchod celým stromem. To znamená, že podle jistého pravidla projdeme celý strom, uzel po uzlu. Pravidla, která určují, jak strom projít, jsou tři:

• Pre order - toto pravidlo nám říká, že při procházení stromem navštívíme nejprve rodiče, poté levého a pravého potomka.
• In order - v tomto případě je nejprve navštíven levý potomek, poté rodič a nakonec pravý potomek.
• Post order - poslední případ je asi jasný - nejprve levý potomek, pak pravý a nakonec rodič.

Verze pro tisk

DISKUZE strom a les 9.11.2010 20:50 Jan Němec Re: strom a les 9.11.2010 23:16 Petr Sklenička Rekurze 13.12.2010 21:39 Aleš Hakl Zobrazit označené Zobrazit vše Příspívat do diskuze mohou pouze registrovaní uživatelé.